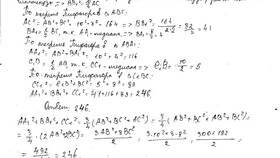Медианы треугольника представляют собой важные элементы его геометрической структуры. Рассмотрим свойства суммы медиан и их взаимосвязь с другими параметрами треугольника.
Содержание
Медианы треугольника представляют собой важные элементы его геометрической структуры. Рассмотрим свойства суммы медиан и их взаимосвязь с другими параметрами треугольника.
Основное свойство медиан треугольника
В любом треугольнике сумма длин трех медиан:
- Всегда больше полупериметра треугольника
- Всегда меньше периметра треугольника
- Связана с длинами сторон определенными соотношениями
Точное соотношение суммы медиан
| Формула | Описание |
| ma + mb + mc > (a+b+c)/2 | Сумма медиан больше полупериметра |
| ma + mb + mc< a+b+c | Сумма медиан меньше периметра |
Формулы для вычисления медиан
Длина каждой медианы вычисляется по формулам:
- ma = ½√(2b² + 2c² - a²)
- mb = ½√(2a² + 2c² - b²)
- mc = ½√(2a² + 2b² - c²)
Свойства точки пересечения медиан
- Точка пересечения медиан делит их в соотношении 2:1
- Эта точка является центром масс треугольника
- Сумма квадратов медиан связана с суммой квадратов сторон
Соотношение между медианами и сторонами
| Свойство | Формула |
| Сумма квадратов медиан | ma² + mb² + mc² = ¾(a² + b² + c²) |
| Связь с площадью | Сумма медиан влияет на площадь через сложные соотношения |
Частные случаи
В специальных типах треугольников сумма медиан имеет особенности:
- В равностороннем треугольнике все медианы равны
- В прямоугольном треугольнике медиана к гипотенузе равна ее половине
- В равнобедренном треугольнике две медианы равны
